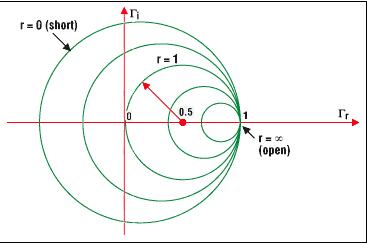
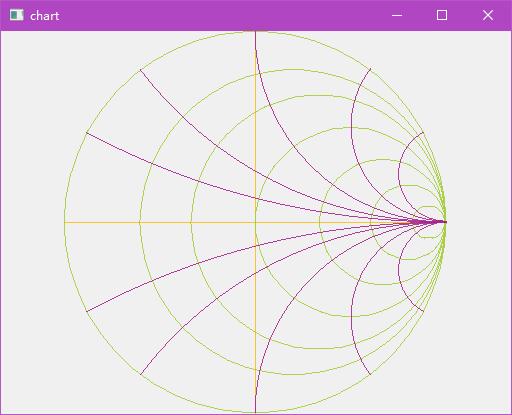
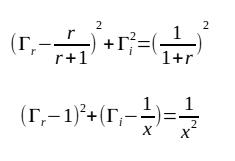1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
| #include "widget.h"
#include <cmath>
#ifndef M_PI
#define M_PI (3.141592653)
#endif
#define LOGIC_WIDTH (435)
#define LOGIC_HEIGHT (435)
#define DEVIDER_CNT (50)
void Widget::paintEvent(QPaintEvent* event) {
QPainter painter(this);
painter.setPen(QColor(Qt::red));
qint16 side = qMin(width(), height());
painter.setViewport((width() - side) / 2,
(height() - side) / 2,
side,
side);
painter.setWindow(0, 0, LOGIC_WIDTH, LOGIC_HEIGHT);
painter.setPen(QColor(253, 189, 19));
painter.drawLine(LOGIC_WIDTH / 2, 0, LOGIC_WIDTH / 2, LOGIC_HEIGHT - 1);
painter.drawLine(0, LOGIC_WIDTH / 2, LOGIC_WIDTH - 1, LOGIC_WIDTH / 2);
painter.setPen(QColor(165, 206, 57));
DrawResistance(painter, 0);
DrawResistance(painter, 0.25);
DrawResistance(painter, 0.5);
DrawResistance(painter, 1);
DrawResistance(painter, 2);
DrawResistance(painter, 4);
DrawResistance(painter, 10);
painter.setPen(QColor(165, 35, 142));
DrawReactance(painter, 0.25);
DrawReactance(painter, 0.5);
DrawReactance(painter, 1);
DrawReactance(painter, 2);
DrawReactance(painter, 4);
DrawReactance(painter, -0.25);
DrawReactance(painter, -0.5);
DrawReactance(painter, -1);
DrawReactance(painter, -2);
DrawReactance(painter, -4);
}
void Widget::DrawResistance(QPainter& painter, float val) {
int x = val / (val + 1) * LOGIC_WIDTH / 2 + LOGIC_WIDTH / 2;
int y = LOGIC_HEIGHT / 2;
int r = 1 / (1 + val) * LOGIC_HEIGHT / 2;
DrawCircle(painter, x, y, r);
}
void Widget::DrawReactance(QPainter& painter, float val) {
int x = LOGIC_WIDTH - 1;
int y = LOGIC_HEIGHT / 2 - 1 / val * LOGIC_HEIGHT / 2;
int r = 1 / abs(val) * LOGIC_HEIGHT / 2;
float r2 = LOGIC_HEIGHT / 2;
float d = sqrt(r * r + r2 * r2);
float phase = acos((r2 * r2 - d * d - r * r) /
(-2 * d * r)) * 2;
phase = phase * 180 / M_PI;
float start = (-90 - phase) * 16;
if (val < 0) {
start = 90 * 16;
}
painter.drawArc(x - r, y - r, 2 * r, 2 * r,
start, phase * 16);
}
void Widget::DrawCircle(QPainter& painter, int x, int y, int r) {
float step = 2 * M_PI / DEVIDER_CNT;
float phase = step;
int prev_x = x + cos(0) * r;
int prev_y = y + sin(0) * r;
int cur_x, cur_y;
for (int i = 1; i <= DEVIDER_CNT; ++i) {
int diff_x = cos(phase) * r;
int diff_y = sin(phase) * r;
cur_x = x + diff_x;
cur_y = y + diff_y;
painter.drawLine(prev_x, prev_y, cur_x, cur_y);
phase += step;
prev_x = cur_x;
prev_y = cur_y;
}
}
|